Inleiding
Gebruik van meetinstrumenten in de klinische psychologie wordt al geruime tijd gepropageerd en hun toepassing in het kader van Routine Outcome Monitoring (ROM) neemt hand over hand toe. Veel professionals in de zorg zijn echter onvoldoende vertrouwd met meetresultaten en voelen zich onvoldoende toegerust om de patiënt goed voor te lichten over de gegevens die ROM oplevert. Het helpt daarbij niet dat de gebruikte meetinstrumenten in de ggz allemaal hun eigen meetschalen hebben en er talloze cryptische afkortingen voor subschalen worden gebruikt. Hierdoor is eerst een grondige studie van het meetinstrument vereist, alvorens iets met de scores aan te kunnen vangen. Een medicus heeft het wat dat betreft iets makkelijker met een enkele schaal voor koorts, een enkele schaal voor bloeddruk en een enkele schaal voor de hemoglobinewaarde van het bloed. Ook is kennis over de interpretatie van scores, met name waar het gaat om verandering in de score over de tijd, nog onvoldoende verspreid. Zo gaapt er een kloof tussen de klinimetrie (het vakgebied dat onderzoek doet naar de kwaliteit van metingen en meetinstrumenten) en de klinische praktijk. Wanneer we patiënten vragen om zelfrapportage meetinstrumenten in te vullen over hun klachten of functioneren, dan moeten we de meetresultaten ook op een begrijpelijke wijze manier uitleggen aan de patiënt. Een professional in de ggz neemt klinische beslissingen om de behandeling voort te zetten, te wijzigen of te stoppen samen met de patiënt en bij voorkeur onderbouwd met een juiste interpretatie van betrouwbare meetgegevens.
Voor dit artikel hebben we ons tot doel gesteld een brug te slaan tussen de psychometrie en de klinische praktijk. We doen dit door een aantal concrete en praktische handvatten te bieden voor hoe meetresultaten vertaald kunnen worden in patiëntvriendelijke en relevante informatie, die gebruikt kan worden in de dagelijkse klinische praktijk. Maar voor we dat kunnen doen, zullen we een paar bekende begrippen uit de psychometrie bespreken. We doen dat aan de hand van een korte casus.
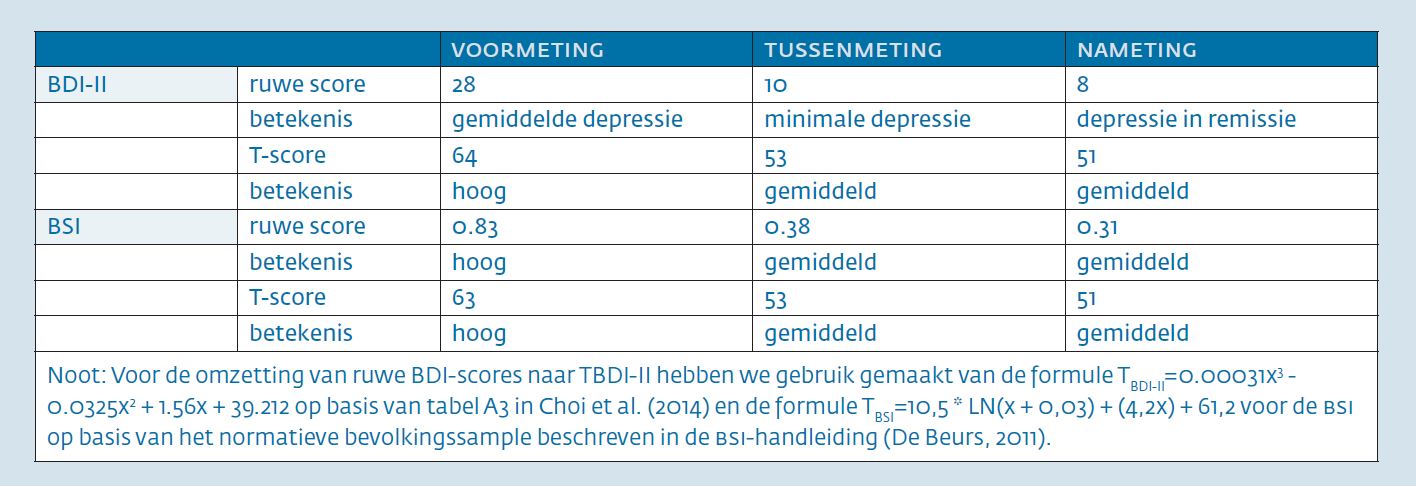
Mevrouw Vermeulen (29) is door haar huisarts verwezen vanwege een depressie. De huisarts heeft een antidepressivum voorgeschreven, maar dat heeft onvoldoende baat opgeleverd en zo is patiënte doorverwezen naar een ggz-instelling. Er wordt besloten tot een behandeling met cognitieve gedragstherapie (CGT) in wekelijkse zittingen. Voorafgaande aan de behandeling zijn twee meetinstrumenten afgenomen: de Beck Depression Inventory (BDI-II) en de Brief Symptom Inventory (BSI). Mevrouw Vermeulen reageert goed op de behandeling: na drie maanden is haar stemming opgeklaard. Samen met haar behandelaar wordt besloten de frequentie van de zittingen terug te brengen tot aanvankelijk tweewekelijks en later maandelijks contact. Weer drie maanden later is het gunstige resultaat van de behandeling in stand gebleven. Drie en zes maanden na de eerste meting zijn dezelfde instrumenten afgenomen voor de evaluatie van de behandeling. De uitslagen van de testafnames op de drie meetmomenten zijn te zien in tabel 1.
Hoe kunnen we deze resultaten nu begrijpen en zinvol met elkaar vergelijken? Voor we hier verder op ingaan, staan we eerst stil bij ruwe scores en gestandaardiseerde T-scores en hoe die zich tot elkaar verhouden.
Ruwe scores en meetschalen
Volgens internationaal onderzoek scoort iemand zonder klachten niet hoger dan 8 op de (Beck & Steer, 1987). 1 Een score van 913 wordt als minimaal depressief beschouwd; een score 1419 als indicatief voor milde depressie, 2028 als gemiddelde en 29 of hoger als ernstige depressie. Een score <9 geeft remissie van depressie aan. Voor de wordt voor vrouwen tot 30 uit de algemene bevolking de volgende betekenis aan scores toegekend: 0.000.06 is zeer laag; 0.070.15 is laag; 0.160.18 is beneden gemiddeld; 0.290.45 is gemiddeld; 0.460.68 is boven gemiddeld; 0.691.55 is hoog; 1.564.00 is zeer hoog (De Beurs, 2011). 5
Een ruwe score op een meetinstrument geeft een positie aan op een schaal. Een schaal heeft een theoretisch bereik: de somscore voor de ernst van de symptomatologie op de Beck Depression Inventory kan een waarde aannemen van 0 tot 63. Bij de Brief Symptom Inventory (; Derogatis, 1975) 10 wordt de totaalscore berekend als de gemiddelde score op 53 items op een vijfpuntschaal en hier heeft de score een theoretisch bereik van 0 tot 4. Een score heeft daarnaast ook een praktisch bereik: de scores die in de klinische praktijk daadwerkelijk worden aangetroffen. Bij de BDI ligt dit praktische bereik tussen de 0 en 55; bij de BSI tussen de 0 en 3. Hogere scores komen nauwelijks voor. Voor elk meetinstrument zijn de meeteenheden en de range van ruwe scores weer anders en dat is niet handig voor het dagelijks gebruik. Er zijn uniforme meetschalen voor psychische concepten voorgesteld, net zoals voor het meten van temperatuur (Celsius), gewicht (grammen) of afstand (kilometers).
T-scores als gemeenschappelijke taal
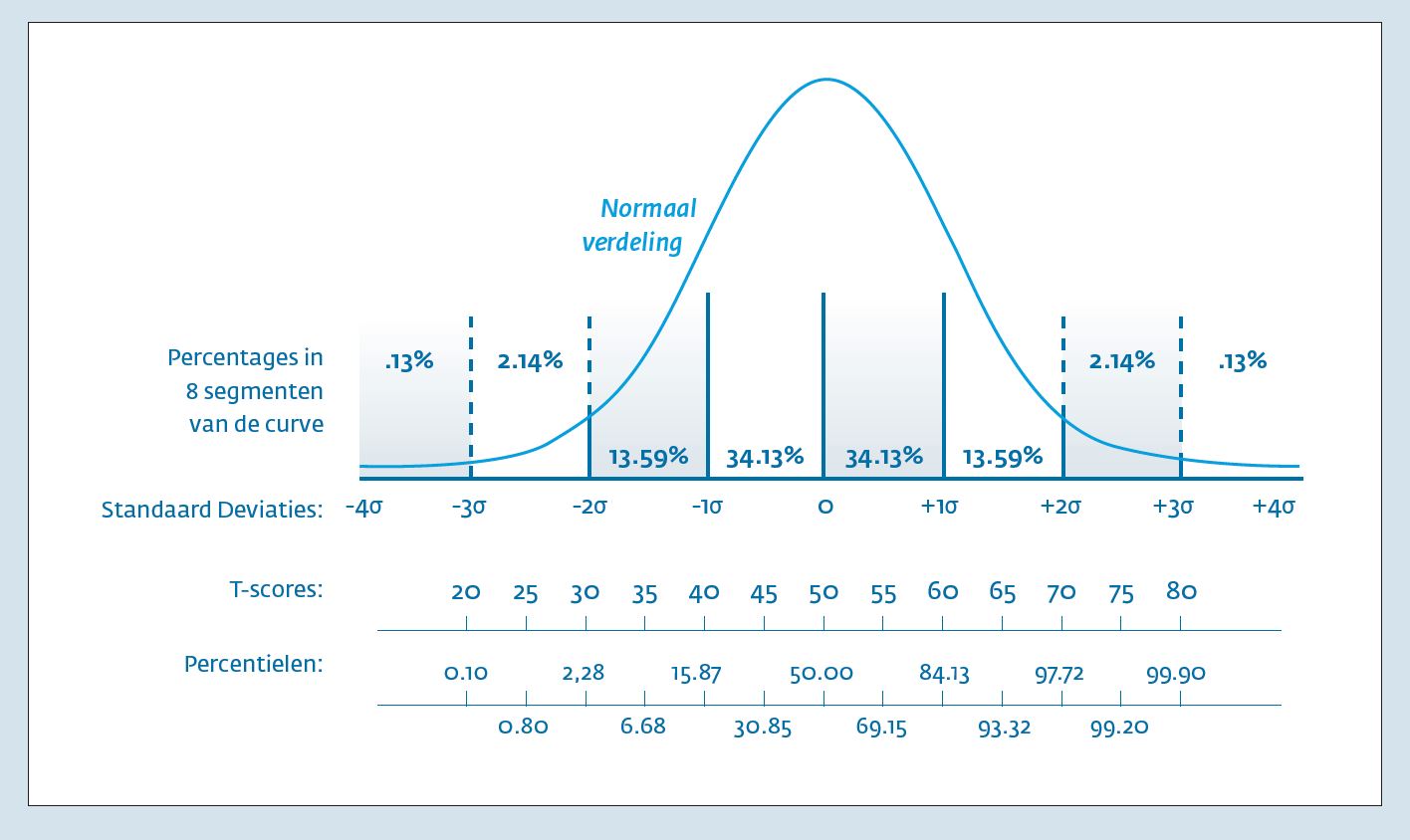
Als uniforme meetschaal of maat voor testuitslagen hebben we eerder de normaal verdeelde T-score voorgesteld (De Beurs, 2010). 4 De T-score heeft een gemiddelde van 50 en een standaarddeviatie van 10 (McCall, 1922). 22 Normaalverdeelde schalen zijn betekenisvol te interpreteren, omdat alle scores een directe relatie hebben met percentielen. Percentielen verdelen een schaal in honderd groepen van gelijke grootte; elk percentiel geeft het percentage personen van de normgroep aan met een lagere score. Een concreet voorbeeld hiervan is de score op de Cito-toets die vaak wordt afgenomen bij kinderen op de lagere school. Heeft een kind een percentielscore van 95 op de Cito-toets behaald, dan had slechts 5% van de leerlingen een hogere score. De percentielschaal geeft dus direct de positie aan in de vergelijkingsgroep. Toegepast op T-scores betekent een score van bijvoorbeeld 70 (2 sd’s hoger dan het gemiddelde) dat 97.7% van de normgroep een lagere score heeft en slechts 2.3% een hogere score heeft.
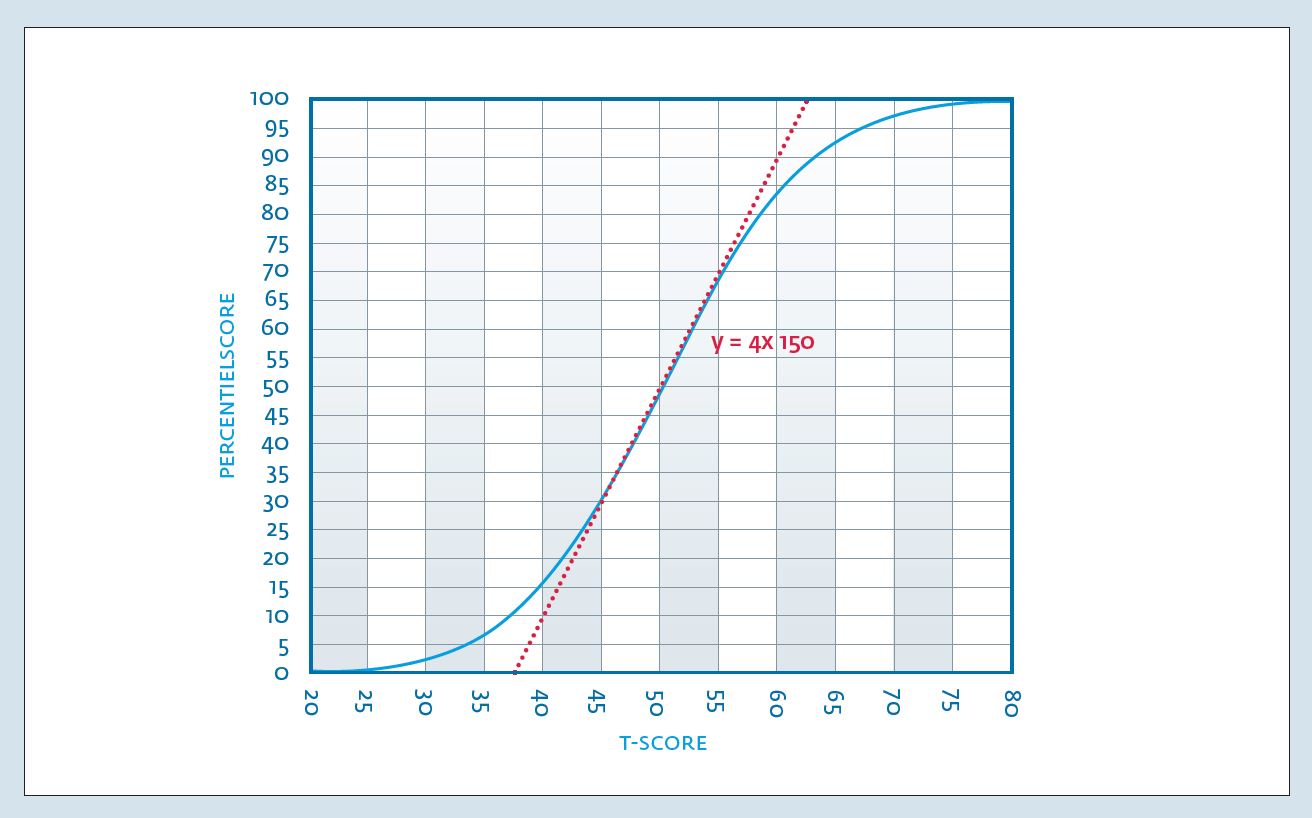
Figuur 1 geeft de normaalverdeling weer en de twee vaak gebruikte schaalverdelingen onder de normaalverdeling, T-scores en percentielscores. Figuur 2 geeft in meer detail de relatie weer tussen T-scores en percentielscores, in feite de cumulatieve normaalverdeling voor μ=50 en σ2=10). Tussen T=45 en 55 is de relatie nagenoeg lineair (de rode stippellijn (y=4×150 is de lineaire relatie; de percentielscore=4*T-score min 150), maar voor hogere of lagere scores is dit verband duidelijk niet lineair. Iemand met een T-score van 60 zou bij een lineair verband een percentielscore van 90 hebben, maar heeft feitelijk een percentielscore van 84.1. Voor T-scores geldt dat 68.3% van de normgroep een score heeft tussen 40 en 60, 95% een T-score tussen 30 en 70 en 99.8% een T-score tussen 20 en 80. Slechts 0.1% van de normgroep heeft een score van 20 of lager en 0.1% een score van 80 of hoger.
Een voordeel van de T-score is dat we het meetniveau mogen beschouwen als een intervalschaal. Percentielscores zijn niet in gelijke intervallen verdeeld over de gehele schaal (zie ook f guur 1 en figuur 2); daarom kunnen T-scores van elkaar worden afgetrokken en percentielscores niet. Voordeel van percentielscores is dat ze in het alledaagse taalgebruik wel makkelijk te begrijpen zijn. Beide type scores kunnen elkaar zo mooi aanvullen.
Betekenis geven aan een enkele score verschillende normgroepen
Verschillende normgroepen
Wie is langer: een vrouw van 175 centimeter of een man van 179 centimeter? Wanneer je ze naast elkaar zet natuurlijk de man. Maar de vrouw is vergeleken met andere vrouwen langer dan de man is vergeleken met andere mannen. De percentielscore voor de vrouw is 75 (slechts 25% van de vrouwen is langer), voor de man is de percentielscore 25 (75% van de mannen is langer). We hebben in dit geval dus een relatief grote vrouw met een relatief kleine man vergeleken.
Dit voorbeeld toont aan dat een score op een algemene meetschaal (centimeters) een absolute betekenis heeft, maar dat je een referentiegroep of normgroep kunt kiezen om een score een relatieve betekenis te geven: een score is hoog, gemiddeld of laag in vergelijking met die normgroep. De betekenis van een score, waaronder ook de T-score, is dus relatief en gebaseerd op een referentiegroep (de normgroep). Dat kan de algemene Nederlandse bevolking zijn of een subgroep daarbinnen, bijvoorbeeld patiënten of mannen en vrouwen. Wat men als referentiegroep kiest, bepaalt de betekenis van de score; scores zijn altijd relatief ten opzichte van een normgroep.
Voor de T-score hebben we eerder voorgesteld patiënten als referentiegroep te nemen (De Beurs, 2010). 4Nadeel van deze insteek is dat niet altijd duidelijk is hoe de normgroep van patiënten is samengesteld (zijn het ambulant behandelde patiënten, opgenomen patiënten, eerstelijns, basis ggz of specialistische ggz-patiënten, patiënten aan het begin of aan het eind van hun behandeling?). En de aard van de referentiegroep is van belang voor een juiste interpretatie van het gevonden meetresultaat.
Sinds 2010 zijn er een aantal ontwikkelingen geweest om meetresultaten te harmoniseren. Voorbeelden zijn het PROMISinitiatief in de Verenigde Staten (Cella et al., 2007), 2 het voorstel van een Duitse groep onderzoekers om depressiematen te standaardiseren (Wahl et al., 2014) 31, het Amerikaanse voorstel om voor bestaande angstmaten een gemeenschappelijke meetschaal te hanteren (Schalet et al., 2014) 26 en het voorstel van ICHOM (Obbarius et al., 2017) 25 om via een conversietabel scores op veelgebruikte meetinstrumenten, zoals de PHQ-9 en de GAD-7 om te zetten van ruwe scores naar T-scores. Hierbij is voor T-scores telkens de algemene bevolking als referentiegroep gekozen. We pleiten ervoor om aan te sluiten bij deze internationale conventie. Voor een goede ijking is het belangrijk dat de bevolkingssteekproef representatief is en qua samenstelling goed overeenkomt met de Nederlandse bevolking (Flens et al., 2017). 15 Een score van 50 is in dat geval de score van de gemiddelde Nederlander en patiënten zullen voorafgaande aan de behandeling meestal tussen de 60 en 70 scoren.
Dit voorstel is al toegepast bij de gegevens in tabel 1 van mevrouw Vermeulen. Zij scoort bij de voormeting 64 en 63 op respectievelijk de BDI-II en de BSI en bij nameting met 51, net 1 punt hoger dan het bevolkingsgemiddelde.
Betrouwbaarheid van de score
De bruikbaarheid van een meetresultaat of score hangt samen met de betrouwbaarheid en de validiteit1 van een meetinstrument. Op validiteit komen we kort terug in een later gedeelte van dit artikel (sectie responsiviteit). De betrouwbaarheid van een meetinstrument wordt op verschillende manieren vastgesteld (Maruyama & Ryan, 2014)2. 21 Dat kan door na te gaan of de scores van verschillende beoordelaars overeenstemmen (interbeoordelaarsbetrouwbaarheid) of door vast te stellen of het meetresultaat bij herhaalde afname van een test hetzelfde blijft (de testhertest betrouwbaarheid), waarbij we ervan uitgaan dat de gemeten respondent in de tussentijd niet verandert. De betrouwbaarheid kan ook bepaald worden door na te gaan of de ene helft van de test hetzelfde resultaat geeft als de andere helft (splithalf betrouwbaarheid). Ten slotte kunnen we vaststellen of de losse items van een instrument onderling samenhangen (interne consistentie van de test). Deze betrouwbaarheidsindex wordt meestal bij zelfrapportagemeetinstrumenten gebruikt en om deze reden bevatten zelfrapportage meetinstrumenten vaak meerdere items die telkens op een iets andere manier naar hetzelfde vragen.
Betrouwbaarheid wordt uitgedrukt in een getal tussen 0.00 en 1.00; hoe hoger de waarde, hoe betrouwbaarder het instrument. Voor uitspraken over groepen patiënten wordt een betrouwbaarheid van r=.70 als goed omschreven (Egberink, Janssen & Vermeulen, 2009). 12 Een relatief onbetrouwbare score per individu in de groep kan toch tot een betrouwbare score van de gehele groep leiden, omdat individuele meetfouten worden uitgemiddeld. Wanneer echter een beslissing over een individuele patiënt genomen moet worden op basis van een score (bijvoorbeeld wel of niet een behandeling starten of staken), dan is een hoger betrouwbaarheidsniveau van minimaal r=.90 vereist (Egberink et al., 2009) 12 of zelfs r=.95 (Nunnally & Bernstein, 1994). 24
De betrouwbaarheid van een individuele score (X=T+E)
Volgens de klassieke testtheorie is de waargenomen score (X) na een testafname bij een individu opgebouwd uit de ware score (T) en een meetfout (E). De meetfout komt tot stand doordat een respondent het item niet goed leest of niet goed begrijpt, etc. Hoe onbetrouwbaarder het instrument, des te groter de meetfout is en des te groter het verschil is tussen de waargenomen score en de ware score. De (on) betrouwbaarheid van de geobserveerde score wordt vaak aangegeven met een soort foutenmarge rondom de gevonden waarde, bijvoorbeeld het 95% betrouwbaarheidsinterval (Confidence Interval of CI95). Dit betrouwbaarheidsinterval wordt zo gekozen dat, als we de test oneindig vaak zouden afnemen, de ware score van de patiënt in 95% van de gevallen binnen het betrouwbaarheidsinterval zal vallen.
De breedte van het betrouwbaarheidsinterval hangt af van de betrouwbaarheid van het instrument en van hoe zeker je wilt zijn (een keuze van de gebruiker voor bijvoorbeeld 80%, 95% of 99%). De breedte van het interval wordt dus in eerste instantie bepaald door de standaardmeetfout van het instrument (Standard Error of measurement of SE). Die waarde wordt weer afgeleid van de spreiding in scores op de meetschaal en de betrouwbaarheidsindex (SE=SD*√(1-r);CI95=T ± 1.96*SE)3.
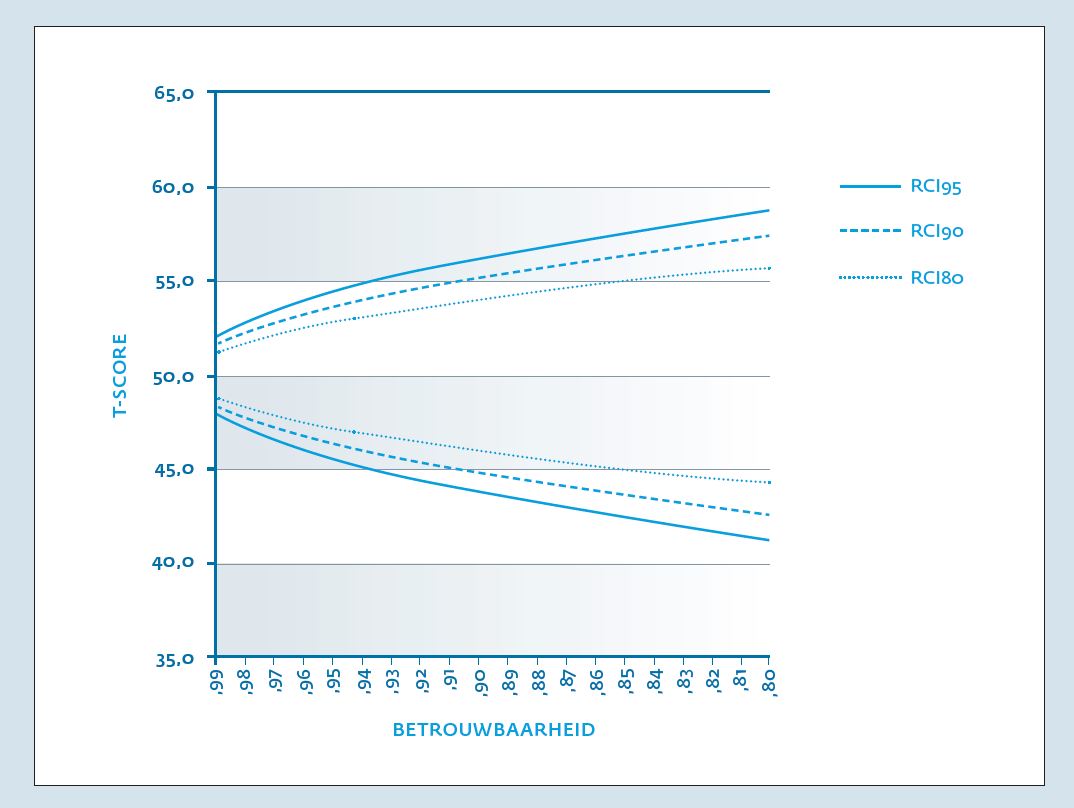
Een voorbeeld met getallen: De SE van T-score waarbij gemeten is met een instrument met een betrouwbaarheid van r=.90 is: 10 * √(1-90) =3.16. Onder de normaalverdeling betekent dit dat er ongeveer 2/3de (het 68% betrouwbaarheidsinterval van deze score of CI68) kans is dat de ware score zich bevindt binnen een interval van ± 3.16 schaalpunt. CI68 is geen gebruikelijk betrouwbaarheidsinterval, CI95 wel. Bij een meetinstrument met een betrouwbaarheid van r=.90 is het 95% betrouwbaarheidsinterval (CI95) ± 6.20; het 90% betrouwbaarheidsinterval (CI90) ± 5.20; het 80% betrouwbaarheidsinterval (CI80) ± 4.05. Hoe zekerder je wilt zijn van de ware score, des te breder het interval wordt: bij een meting met een betrouwbaarheid van r=.90 weten we bij een score van 50 met 80% zekerheid dat de ware score zich bevindt tussen 45.95 en 54.05 en met 95% zekerheid dat de ware score zich bevindt tussen 43.80 en 56.20. De omvang van het betrouwbaarheidsinterval is dus afhankelijk van de gewenste zekerheid van een juiste uitspraak. Met 100% zekerheid kunnen we stellen dat de ware score van een patiënt tussen oneindig en +oneindig zal liggen, maar dat is niet erg informatief. Naast de gewenste zekerheid (95, 90 of 80%) bepaalt ook de betrouwbaarheid van het meetinstrument de omvang van het betrouwbaarheidsinterval. Figuur 3 geeft de relatie weer tussen de betrouwbaarheid van een test (op de x-as) en drie betrouwbaarheidsintervallen (CI95, CI90 en CI80) van het meetresultaat uitgedrukt in T-scores. We zien in figuur 3 dat pas bij een testbetrouwbaarheid van r>.93 een betrouwbaarheidsinterval van ±5 T-score punten bereikt wordt. Bij een betrouwbaarheidscoëfficiënt van r=.99 is het 95% betrouwbaarheidsinterval (CI95) ±2 T-score punten.
De betrouwbaarheid van een meting bij een individu neemt toe als we vragen stellen die relevant zijn voor het te meten concept en goed aansluiten bij de problematiek van de patiënt (items met een hoge informatiewaarde). Verder neemt de betrouwbaarheid toe naarmate we herhaaldelijk naar min of meer hetzelfde vragen (door bijvoorbeeld meer items toe te voegen aan het meetinstrument). Hiermee wordt ook duidelijk dat instrumenten die maar uit een enkel item bestaan (bijvoorbeeld de GAF-score van de DSM-IV) eigenlijk geen betrouwbare informatie op kunnen leveren over een individuele patiënt.
Het betrouwbaarheidsinterval rondom een meetresultaat geeft aan tussen welke waarden de ‘ware’ score van patiënt zich meestal zal bevinden. Het 95% betrouwbaarheidsinterval bij een testbetrouwbaarheid van r=.95 geeft een interval van ± 4.4 T-score punten rond de gevonden waarde; het 90% betrouwbaarheidsinterval bij een testbetrouwbaarheid van r=.95 geeft een interval van ± 3.7 T-score punten; het 90% betrouwbaarheidsinterval bij een testbetrouwbaarheid van r=.90 geeft een interval van ± 5.2 T-score punten. (Bij de eerste auteur van het artikel is een brochure voor de patiënt op te vragen waarin met foutbalken het 95% betrouwbaarheidsinterval is aangegeven.)
Wanneer is een score te hoog, gemiddeld of te laag
Hoe verfijnd we betekenis aan een score kunnen toekennen, hangt af van de precisie van de meting. De precisie of de betrouwbaarheid wordt uitgedrukt in de standaardmeetfout of de Standard Error of measurement (SE). Bij een relatief onbetrouwbare meting kunnen we bij het geven van een betekenis aan de score niet verder gaan dan een indeling in drie niveaus: laag (T < 45; 031%), gemiddeld (T 45–55; 3169%) en hoog (T > 55; 69 tot 100%).
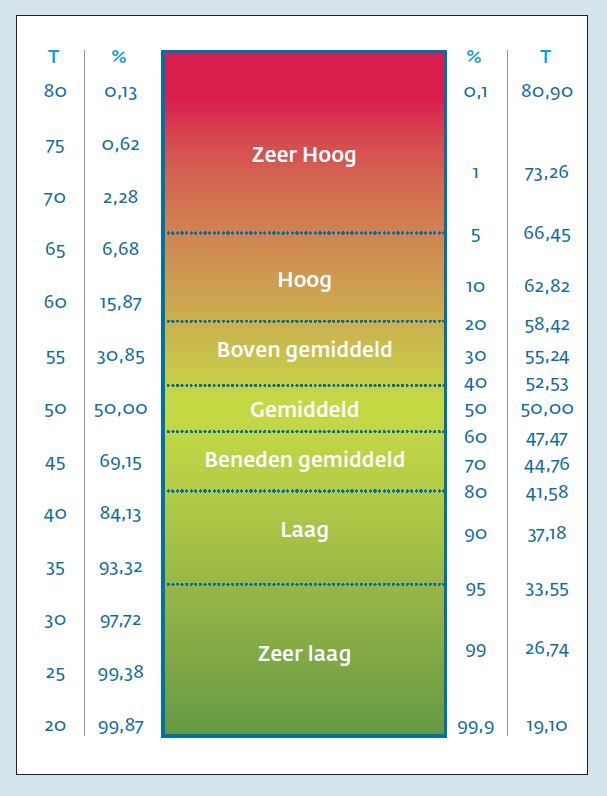
Bij een meer betrouwbare meting is een indeling in zeven categorieën gebruikelijk. Percentages in de populatie worden dan doorgaans als volgt omschreven: zeer laag (05%), laag (520%), beneden gemiddeld (2040%) gemiddeld (4060%) boven gemiddeld (6080%), hoog (8095%) en zeer hoog (95100%). Omdat de normaal verdeelde T-scores een directe relatie hebben met percentielscores kunnen deze niveaus zowel in T-scores als in percentielscores worden uitgedrukt. Dit wordt weergegeven in figuur 4 voor zeven niveaus. Links staan T-scores en corresponderende cumulatieve percentages; rechts percentielen en corresponderende T-scores; in het midden staan betekenissen die aan een score worden gegeven wanneer men zeven niveaus hanteert. Zeven niveaus hanteren vergt overigens wel aanzienlijke precisie van het instrument; bij een meetinstrument met een grote meetfout is het bijvoorbeeld onzinnig om onderscheid te maken tussen een gemiddelde en een bovengemiddelde score.
Verandering over de tijd
In de klinische praktijk monitoren we niet alleen om te weten te komen hoe hoog een patiënt scoort ten opzichte van een normgroep, maar willen we ook vaststellen of in de loop van de tijd de score betekenisvol verandert. Dan weten we of de behandeling aanslaat of niet. Als er niets verandert in de scores, dan is dat iets om te bespreken met de patiënt en kunnen behandelaar en patiënt overwegen om de behandeling over een andere boeg te gooien, zoals een ander medicament of een andere behandelmodaliteit of de behandeling staken. Als er juist wel iets verandert in de scores, dan kan de behandelaar evalueren met de patiënt of de behandeldoelen zijn behaald en de behandeling daarmee afgerond kan worden. Hoe kunnen meetresultaten hierbij helpen?
De score van mevrouw Vermeulen op de BDI-II veranderde van 64 bij de voormeting naar 53 bij de tussenmeting en naar 51 bij de nameting. Wat betekent een verschuiving met 11 punten? En is de tweede verschuiving met 2 punten nog betekenisvol?
Betekenis toekennen aan verandering in score over tijd
Bij het vergelijken van twee scores geeft de verschilscore de mate van verandering aan. Om scores van elkaar af te mogen trekken is een normaal verdeelde schaal vereist. Is de schaal niet normaal verdeeld, dan is een verschil tussen twee scores in het lage scoregebied bijvoorbeeld niet hetzelfde als een verschil tussen twee scores in het hoge scoregebied.
Een uitwerking met een concreet getallenvoorbeeld van dit probleem en de wijze waarop T-scores hier een oplossing voor bieden is te vinden in De Beurs (2010) 4 of De Beurs en Flens (2017). 6 Het omzetten van ruwe scores naar de normaal verdeelde T-scoreschaal is dus niet alleen een goed idee om individuele scores betekenis te geven; het is zelfs noodzakelijk om verschilscores tussen twee metingen te mogen berekenen (De Beurs, 2010). 4 Percentielscores – hoewel intuïtief aantrekkelijk – mogen überhaupt niet van elkaar worden afgetrokken.
Responsiviteit
Wanneer we in de klinische praktijk willen meten of een behandeling effect heeft en tot verbetering heeft geleid, speelt een ander belangrijk kenmerk van een meetinstrument een rol: de responsiviteit of de gevoeligheid om verandering te detecteren. De responsiviteit wordt bepaald door de validiteit van het meetinstrument en door de betrouwbaarheid.
Om met de validiteit te beginnen: een meetinstrument is responsiever naarmate het beter meet wat is beoogd te bereiken met de behandeling. Zo toonden Dingemans en Van Furth (2017) 11 recent aan dat bij patiënten met een eetstoornis de Eating Disorders Evaluation Questionnaire (EDEQ) aanzienlijk responsiever is dan de Brief Symptom Inventory (De Beurs & Zitman, 2006). 8 De meetinstrumenten meten ook verschillende constructen: eetstoornissymptomatologie en algemene psychopathologie. De resultaten wijzen uit dat het ene construct meer verandert dan het andere. Bij een eetstoornis is de dus beter geschikt om verandering in symptomatologie te meten dan de BSI.
Generieke schalen, zoals de totaalscore op de BSI of de OQ-45 blijken over het algemeen minder responsief dan meetinstrumenten die zijn toegesneden op een specifieke doelgroep of het specifieke probleem dat behandeld wordt (Van der Mheen et al., 2017) 30. Deze algemene uitspraak behoeft echter wel enige nuancering: specifieke subschalen van de BSI en de OQ-45 blijken veel responsiever dan de meer globale totaalscore op deze meetinstrumenten en komen qua responsiviteit in de buurt van stoornisspecifieke meetinstrumenten voor stemmings of angststoornissen (De Beurs et al., 2018 7 ; Schawo et al., 2019 27 ).
Opnieuw betrouwbaarheid
De betrouwbaarheid van het meetinstrument is medebepalend voor de responsiviteit. Aan een onbetrouwbare meting is weinig af te lezen, zoals is gebleken in onze eerdere uitleg over betrouwbaarheid. Dit geldt ook voor het detecteren van verandering over tijd. Een kleine verandering over de tijd kan berusten op een toevallige fluctuatie in score. Zo’n toevallige fluctuatie kan optreden vanwege onbetrouwbaarheid van het meetinstrument. Scores schommelen nu eenmaal over de tijd binnen hun betrouwbaarheidsinterval. Bij een grote verandering in score kunnen we met meer zekerheid concluderen dat we te maken hebben met een werkelijke verandering in ernst, dan bij een kleine verandering in score.
Maar hoe groot moet de scoreverandering zijn om er redelijk zeker van te zijn dat we een betrouwbare verandering zien? Jacobson en collega’s (Jacobson & Revenstorf, 1988 16 ; Jacobson et al., 1999) 17 hebben hiervoor een methode ontwikkeld.
Statistisch betrouwbare verandering
Als het verschil tussen twee scores groter is dan een toevallige schommeling vanwege meetonbetrouwbaarheid, dan spreken we van een statistisch betrouwbaar verschil. Een kleinere verandering is toe te schrijven aan onbetrouwbaarheid van de verschilscore; een grotere verandering is ‘echt’ en wordt ook wel Reliable Change genoemd. De grenswaarde voor betrouwbare verandering op een instrument heet de Reliable Change Index (RCI). Tabel 2 biedt een overzicht van RCI-waarden bij vier testbetrouwbaarheden (r=.97, 95 en 90) en bij diverse niveaus van zekerheid dat je een juiste uitspraak doet (bijvoorbeeld RCI95, RCI90 of RCI80)4. Een verandering in T-score op de BSI tot 4.8 punten kan toegeschreven worden aan meetonbetrouwbaarheid, en vanaf 5 of meer is er met 95% zekerheid een statistisch betrouwbare verandering bereikt.
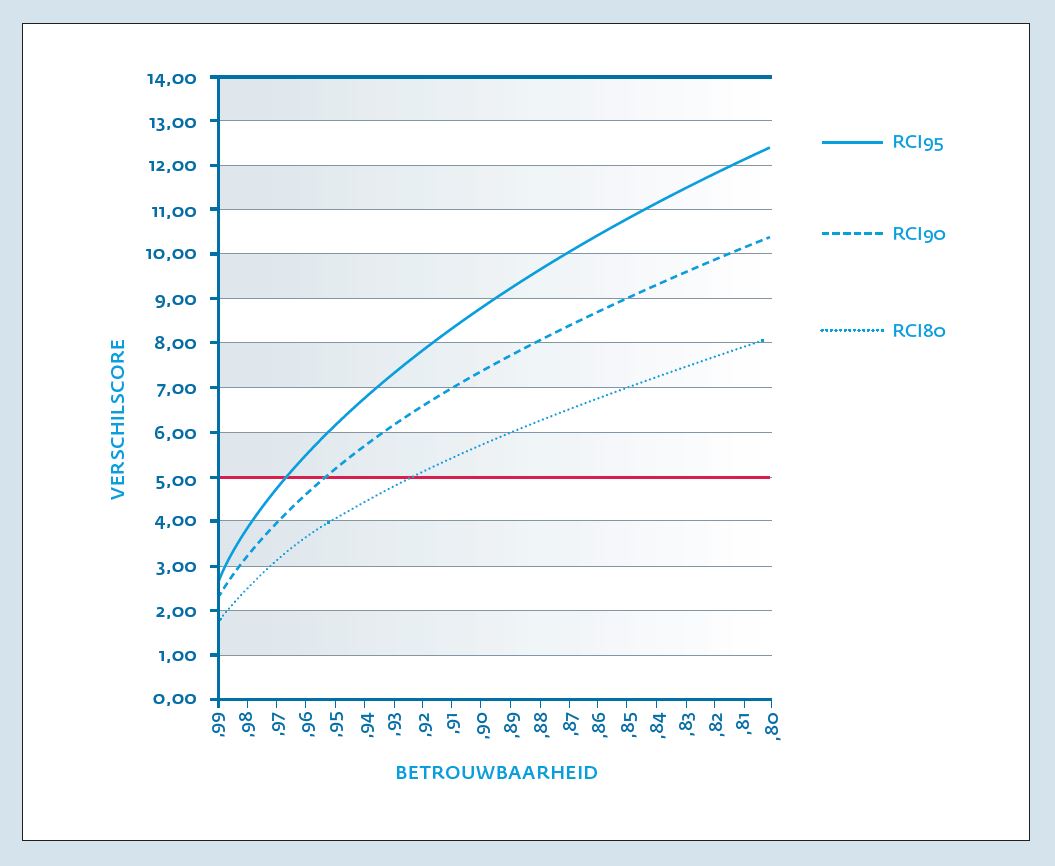
Figuur 5 biedt deze informatie ook, maar nu voor meer betrouwbaarheidscoëfficiënten. Met figuur 5 is vast te stellen hoe groot de verschilscore moet zijn bij een bepaalde betrouwbaarheid van de testscore om met 80%, 90% of 95% zekerheid vast te stellen dat er sprake is van een statistische betrouwbare verandering. Als de test een betrouwbaarheid heeft van r=.95 (weergegeven op de xas), dan kunnen we bij een verschilscore (weergegeven op de yas) van 5.20 of meer met 90% zekerheid (RCI90) aannemen dat de patiënt werkelijk veranderd is; er is 10% kans dat ten onrechte wordt geconcludeerd dat de patiënt veranderd is.
We stellen voor als grenswaarde voor betrouwbare verandering een verschil van meer dan 5 punten5. Dit is een halve standaarddeviatie en komt qua omvang overeen met wat een minimaal waarneembare verandering is (‘minimally detectable’ en ‘minimally important di¥erence’; Jaeschke, Singer & Guyatt, 1989 18 ; Norman, Sloan & Wyrwich, 2003 23 ; Sloan, Cella & Hays, 2005 28 ).6 Dit veronderstelt bij 90% zekerheid over een juiste uitspraak een zeer betrouwbaar meetinstrument (op zijn minst r=.95). De meeste gebruikte meetinstrumenten in de klinische psychologie halen dit betrouwbaarheidsniveau niet. Bij geringere betrouwbaarheid van het instrument is een verschil van 5 punten te weinig en zou de grens eerder op 10 punten of nog hoger moeten liggen. Dit onderstreept nog eens de noodzaak om betrouwbare meetinstrumenten te gebruiken voor uitspraken over individuen.
Klinisch betekenisvolle verandering
Een tweede concept dat Jacobson en collega’s hebben geïntroduceerd gaat over de klinische betekenis van verandering. Een patiënt kan statistische betrouwbaar veranderen (verbeteren), maar bij de nameting nog steeds een hoge score hebben. Van klinisch betekenisvolle verandering (Clinical Significance of CS) spreken ze wanneer de score van een respondent niet alleen statistisch betrouwbaar verandert, maar ook een grensscore passeert die de overgang van ziek naar gezond markeert. Deze grensscore kan berekend worden volgens de formule CS=s2*M1+ s1*M2 / s1+s2 .
Bij gebruik van een meetinstrument waarop de zieke populatie bij de voormeting gemiddeld T=65 scoort en de gezonde populatie T=50 zouden we dit snijpunt op 57.5 kunnen stellen. In onderzoek naar de bruikbaarheid van meetinstrumenten voor screeningsdoeleinden worden vaak optimale afkappunten voorgesteld, bijvoorbeeld voor algemene psychopathologie: BSI>0.58 (De Beurs, 2011) 36 ; OQ-SD-SD>34’(Timman, De Jong & De Neve-Enthoven, 2017) 29 ; voor depressie: PHQ-9>8; CES-D.18; BDI-II.17 ‘voor Angststoornissen: MASQ-GA>23; GA D-7; Panas>21 (Choi et al., 2014 3 ; Schalet et al., 2014 26 ; Wahl et al., 2014) 31. Na T-score transformatie liggen deze afkappunten allemaal rond de 60. PROMIS gebruikt als afkappunt T=55. Een grenswaarde van T=55 is strenger dan de grenswaarden voor ‘caseness’ op veelgebruikte instrumenten en iets lager dan de berekende waarde, maar een veilige keuze, totdat we zeker weten dat succesvol behandelde patiënten in meerderheid onder de T=60 of T=57.5 scoren.
Klinische behandeluitkomst
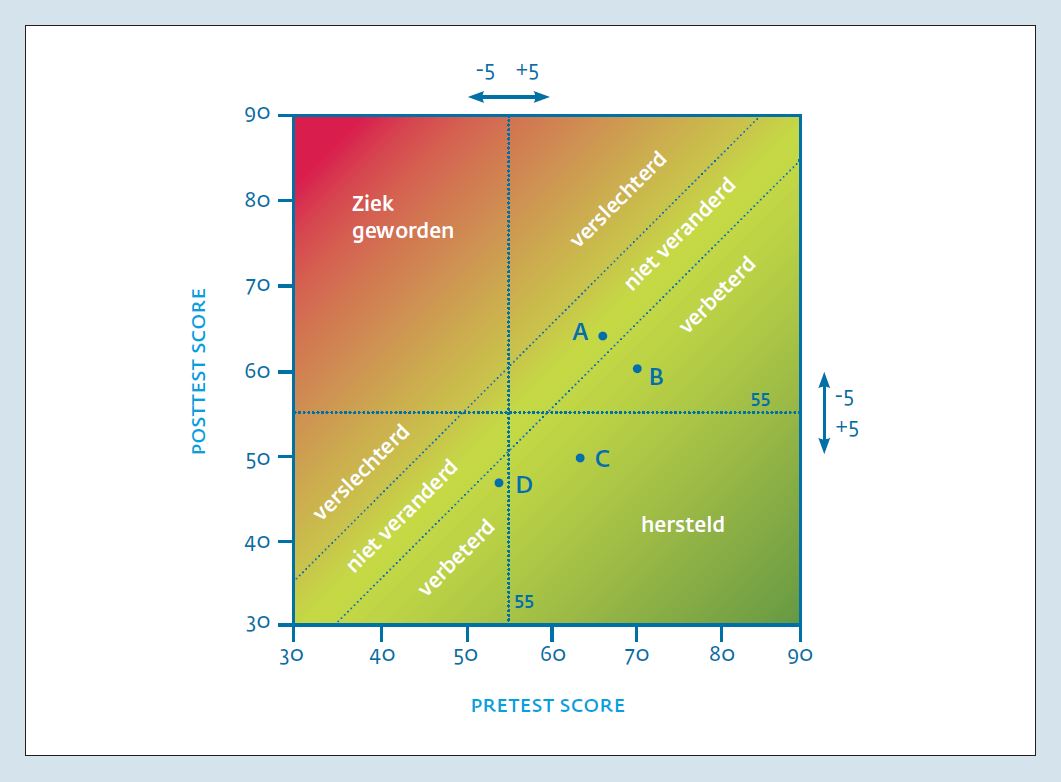
Gebruik van beide grensscores (verschilscore > 5 en overschrijden van de grensscore CS=55) levert vijf klinisch herkenbare behandeluitkomsten op: de respondent is hersteld (zowel RCI als CS), verbeterd (alleen RCI), niet veranderd (de verandering is kleiner dan ), verslechterd (alleen RCI, maar in de ‘verkeerde’ richting) en ziek geworden (zowel RCI als CS). De laatste twee categorieën komen minder voor en kunnen samengenomen worden.
De uitkomsten zijn schematisch weergegeven in figuur 6. De voormetingscore staat op de x-as en de nametingscore op de y-as. In figuur 6 wordt een patiënt met een nagenoeg gelijke score bij voor- en nameting (respectievelijk 67 en 64) geplaatst in de diagonale band ‘niet veranderd’ (patiënt A). Een patiënt met een score bij de voormeting van 70 en bij de nameting van 60 valt in het ‘verbeterd’ gebied (patiënt B). Een patiënt met een voormeting score van 63 en een nameting score van 50 is ‘hersteld’ (patiënt C).
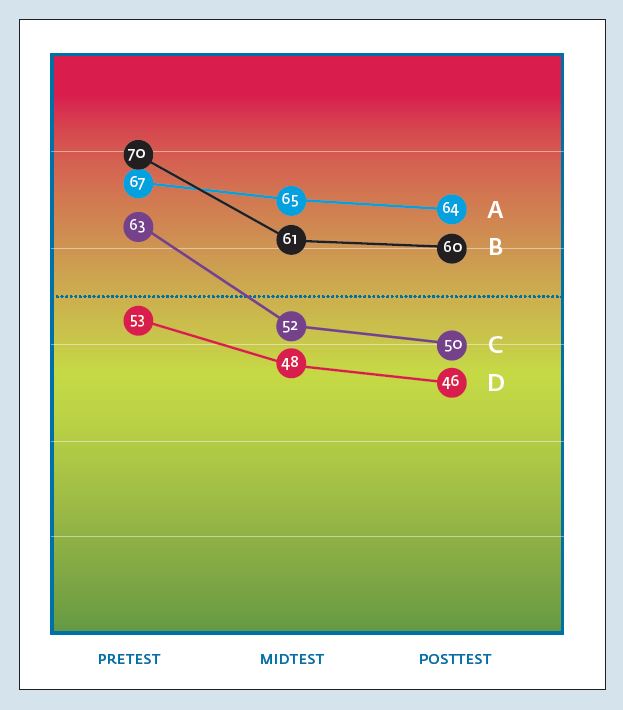
Ten slotte zijn de scores weergegeven van een patiënt met een voormetingscore van 53 en een nametingscore van 46; deze patiënt scoorde bij de voormeting al onder de grensscore en is dus alleen verbeterd (patiënt D). Figuur 7 illustreert het verloop van klachten over de tijd bij dezelfde vier patiënten met nu ook hun scores halverwege de behandeling.
Nieuwe ontwikkelingen
Ter ondersteuning van klinische beslissingen bij individuele patiënten (continueren of stoppen, op of afschalen van de behandeling) zijn uiterst betrouwbare en valide meetinstrumenten noodzakelijk. Een betrouwbaarheid van r=.70 of .80 is voor het vergelijken van gemiddelde scores van groepen patiën acceptabel, maar voor bruikbare informatie over individuele patiënten moet de betrouwbaarheid van het instrument hoger zijn, bij voorkeur r=.95 of hoger.
Een hoge betrouwbaarheid kan gerealiseerd worden met veel items, maar lange meetinstrumenten zijn niet klantvriendelijk en te veel vragen stellen over hetzelfde brengt het risico met zich mee dat de respondent na veel gelijksoortige items de beantwoording niet meer serieus ter hand neemt. Recent is er een meetmethode geïntroduceerd in de Nederlandse ggz om tegemoet te komen aan dit dilemma: computergestuurd adaptief testen (CAT). Deze meetmethode is op de Item Respons Theorie gebaseerd en behelst dat uit een verzameling van items (een zogenaamde itembank) vragen worden voorgelegd tot een score met een hoge betrouwbaarheid is bereikt. Gaandeweg de test worden steeds beter passende items aangeboden. Met zes tot acht vragen is zo een meetbetrouwbaarheid van r=.95 of meer te behalen. Hiermee kunnen we goed uit de voeten om verandering bij individuele patiënten statistisch betrouwbaar vast te stellen. Een uitgebreide bespreking van CAT valt buiten het bestek van dit artikel, maar is recent geboden door Flens en De Beurs (2017) 14 en door Williams, Flens & De Beurs (2017). 32 Inmiddels is de validatie van CAT’s voor depressie en angst voor het Nederlandse taalgebied bijna afgerond en zijn CAT’s in ontwikkeling voor tal van andere aan gezondheid gerelateerde concepten, waaronder het functioneren.
Ter afsluiting
Samenvattend hebben we zes aanbevelingen gedaan:
- We stellen opnieuw de T-score voor als universele maat voor testresultaten van klinische meetinstrumenten, echter nu geijkt op de algemene bevolking;
- Voor het meten van individuen in de ggz is de betrouwbaarheid van het meetinstrument bij voorkeur minimaal r=.95; rond de T-score presenteren we het ˆ‘95 betrouwbaarheidsinterval;
- We gebruiken zeven betekenisniveaus (5, 20, 40, 60, 80 en 95 percentiel), met omschrijvingen van ‘zeer laag’ tot ‘zeer hoog’.
- Op de T-score meetschaal is een verandering van meer dan 5 punten statistisch 90% betrouwbaar.
- De grensscore voor de overgang van ziek naar gezond is T=55;
- Om de behandeluitkomst klinisch betekenisvol te duiden stellen we vijf categorieën voor: hersteld (zowel RCI90 als CS), verbeterd (alleen RCI90), niet veranderd (de verandering is kleiner dan RCI90), verslechterd (alleen RCI90, maar in de ‘verkeerde’ richting) en ziek geworden (zowel RCI90 als CS).
We hopen met deze aanbevelingen een bijdrage te leveren die leidt tot meer uniformiteit in hoe we meetresultaten in de ggz interpreteren. Uniformiteit komt een goed begrip van meetresultaten ten goede en kan leiden tot een toename van het gebruik van meetinstrumenten in de klinische praktijk. Essentieel voor een brede invoering van ROM in de ggz is optimale ondersteuning van de behandelaar met bruikbare en toegankelijke software. Om die reden roepen we ontwikkelaars van software graag op om bij het presenteren van meetresultaten onze aanbevelingen in hun applicaties door te voeren. Ten slotte hopen we met dit artikel testontwikkelaars aan te moedigen om het meetinstrumentarium te verbeteren en opleiders om aan te sturen op verantwoord testgebruik.