Sir Harold Jeffreys en de freudiaanse psychoanalyse
De lange wetenschappelijke carrière van Sir Harold Jeffreys (1891-1989) wordt gekenmerkt door fundamentele bijdragen in de seismologie, geofysica, astronomie, wetenschapsfilosofie en Bayesiaanse statistiek. Jeffreys publiceerde daarnaast artikelen over wiskunde, kwantummechanica, relativiteitstheorie, plantkunde, fotografie en psychologie. Zijn gebundelde werk beslaat meer dan 3600 pagina’s, gelardeerd met wiskundige vergelijkingen. Behalve 440 wetenschappelijke artikelen publiceerde Harold Jeffreys ook nog acht invloedrijke boeken. Kortom: Jeffreys was zonder twijfel een van de meest veelzijdige wetenschappelijke genieën van de twintigste eeuw.

In weerwil van zijn zuiver wetenschappelijke instelling heeft Jeffreys het grootste deel van zijn leven de freudiaanse psychoanalyse aangehangen en uitgedragen. De directe aanleiding hiervoor is verloren gegaan in de nevelen der tijd, maar het zou iets te maken kunnen hebben met Jeffreys’ toenmalige collega en verloofde Dorothy Wrinch (1894-1976), die rond 1920 haar relatie met Jeffreys verbrak. Vaststaat dat Jeffreys rond die tijd zelf ook een psychoanalytische behandeling heeft ondergaan.
In de wetenschapsfilosofie wordt de freudiaanse psychoanalyse steevast aangehaald als schoolvoorbeeld van hoe wetenschap níet bedreven moet worden. De psychoanalyse gaat gebukt onder een gebrek aan duidelijk toetsbare voorspellingen, derhalve valt de methode nauwelijks met empirische data te ondersteunen of te ontkrachten (voor recente samenvattingen zie Paris, 2017, en van Rillaer, 2021).
Jeffreys zelf wees dergelijke kritiek stellig van de hand: ‘Dit is slechts een kwestie van weigeren te onderzoeken en maakt geen indruk op de analyticus die dagelijks met het materiaal te maken heeft, of op de patiënt die genezen is van verschillende geestelijke stoornissen, variërend van kleine angsten tot fobieën of invaliderende neuroses, doordat hij in staat is gesteld om zijn eigen mentale processen beter te begrijpen.’ (Jeffreys, 1931, p. 204)
In 1936 combineerde Jeffreys zijn interesse voor getallen met zijn fascinatie voor de psychoanalyse. Dit resulteerde in een opmerkelijk artikel over de ‘mannelijkheid’ en ‘vrouwelijkheid’ van bepaalde getallen. De kern van Jeffreys’ betoog luidt als volgt: ‘Als we eenmaal de onbewuste aard van het belang van bepaalde getallen hebben ingezien, kunnen we onze kennis uit de psychoanalyse en de observatie van kinderen gebruiken om deze te interpreteren. De eerste objecten die de baby interesseren zijn de borsten en het mannelijk orgaan, de eerste twee in getal, de laatste driedelig; en de fallische symboliek van objecten als het klavertje, de fleur de lis [lelie, red.] en de vlieg is duidelijk. Dit leidt ons rechtstreeks naar de suggestie dat even getallen voor het onbewuste vrouwelijk zijn en oneven mannelijk. Dit verklaart meteen de kracht die geassocieerd wordt met oneven getallen in termen van de kracht van de penis, oorspronkelijk in urineren, later in erectie en geslachtsgemeenschap; het ‘geluk’ symboliseert uiteindelijk het bezit van de penis. Het gevaar drukt voor de jongen het gevaar uit van het verlies van de penis als straf voor een of andere verboden wens of daad, en voor beide seksen een mogelijke verwonding door de penis van de vader. Even getallen brengen geen geluk, maar het meisje, dat geen penis bezit, loopt geen gevaar deze te verliezen, zodat ze veilig zijn.’ (Jeffreys, 1936, p. 218)
Dit betoog is weliswaar hoogst speculatief, maar onderscheidt zich toch van veel andere psychoanalytische theorieën in die zin dat Jeffreys een concreet toetsbare voorspelling doet: even getallen zijn geassocieerd met vrouwelijkheid, en oneven getallen zijn geassocieerd met mannelijkheid.
Het is opmerkelijk dat een wetenschapper van het kaliber van Jeffreys zijn voorspelling niet aan de empirie heeft willen toetsen, maar wellicht vond hij de geopperde associatie zo evident dat ze geen empirische ondersteuning nodig had, of Jeffreys meende misschien dat zijn tijd beter besteed was aan het ontrafelen van de structuur van de aardkern met behulp van wiskundige modellen en seismologische data.
Eerdere bevindingen

De voorspelling van Jeffreys is al eerder empirisch getoetst. In 2015 vroegen Jim Wilkie en Galen Bodenhausen 119 studenten de cijfers 0 tot en met 9 te scoren op mannelijkheid en vrouwelijkheid. De bevindingen waren grotendeels consistent met Jeffreys’ voorspelling (hoewel nergens uit blijkt dat de auteurs van Jeffreys’ theorie op de hoogte waren): ‘Oneven getallen leken mannelijk, terwijl even getallen vrouwelijk leken. Hoewel zowel mannen als vrouwen dit patroon vertoonden, was het meer uitgesproken bij vrouwen.’ In andere experimenten vonden Wilkie en Bodenhausen vergelijkbare resultaten.
Om een meer gedetailleerd beeld te krijgen van dit fenomeen hebben we drie grootschalige online vragenlijst-studies opgezet die afgenomen zijn door KiesKompas. Alle deelnemers werd gevraagd naar hun genderidentiteit en alleen de antwoorden van mannen en vrouwen worden hieronder (apart) gepresenteerd. De data zijn publiekelijk beschikbaar op https://osf.io/ut7rx/.
De Eerste Vragenlijst: Beoordeling van Individuele Cijfers
In de eerste vragenlijst werd 3829 respondenten gevraagd de cijfers 0 tot en met 9 te beoordelen op een schaal van ‘erg vrouwelijk; (waarde 0) tot ‘erg mannelijk’ (waarde 100). De cijfers werden in willekeurige volgorde aangeboden.
Resultaten
Figuur 1 toont de gemiddelde resultaten apart voor de 1689 mannelijke en 908 vrouwelijke respondenten die alle cijfers van een oordeel voorzagen. Zowel mannen als vrouwen vinden de 1 en de 5 relatief mannelijk en de 2 licht vrouwelijk, maar daar houdt de overeenstemming ook wel op. Mannen vinden de 3 relatief vrouwelijk, en de 7, 8, en 9 relatief mannelijk, terwijl vrouwen de 6, 8 en 9 juist als relatief vrouwelijk beoordelen. Voor de vrouwen (maar niet voor de mannen) is er een duidelijk zigzag-patroon, waarin de even cijfers telkens als vrouwelijker worden beoordeeld dan de daaraan voorafgaande oneven cijfers.
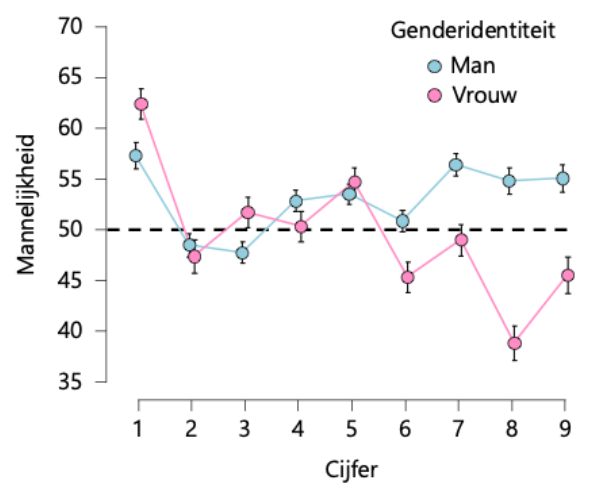
Figuur 1. Gemiddelde mannelijkheidsscores (minimum 0, maximum 100) voor de cijfers 1 tot en met 9, apart voor 1689 mannelijke en 908 vrouwelijke respondenten. De onzekerheid rondom de gemiddelde scores is weergegeven middels een 95 procents-betrouwbaarheidsinterval; wanneer dit interval niet overlapt met de zwarte stippellijn (die een neutrale score van 50 weergeeft), dan is het resultaat “statistisch significant”. De y-as is afgesneden zodat de verschillende uitkomsten visueel beter met elkaar vergeleken kunnen worden. De figuur (CC-BY) is gemaakt met JASP (jasp-stats.org).
Figuur 2 toont de resultaten gemiddeld voor de even en oneven cijfers. De vrouwelijke respondenten vinden oneven cijfers relatief mannelijk, en even cijfers relatief vrouwelijk. Dit komt overeen met de voorspelling van Jeffreys. Hierop valt het volgende af te dingen:
- de mannelijke respondenten vinden zowel de oneven als de even cijfers meer mannelijk;
- bij de vrouwelijke respondenten weerspreekt het meer gedetailleerde patroon van Figuur 1 de algemene psychoanalytische voorspelling van Jeffreys;
- het getoonde patroon betreft de gemiddelde scores over een grote groep – de scores van de individuele respondenten zijn erg variabel (hier niet getoond), terwijl de psychoanalytische onderbouwing impliciet aanspraak doet op een algemene wetmatigheid.
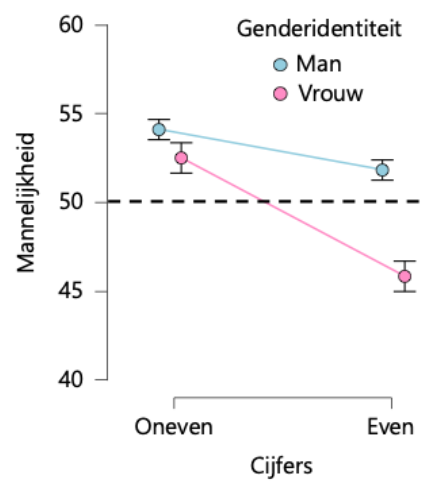
Figuur 2. Gemiddelde mannelijkheidsscores (minimum 0, maximum 100) voor de cijfers 1 tot en met 9, apart voor 2477 mannelijke en 1352 vrouwelijke respondenten (omdat deze analyse ook incomplete data meeneemt, zijn de aantallen groter dan die in Figuur 1). De onzekerheid rondom de gemiddelde scores is weergegeven middels een 95 procents-betrouwbaarheidsinterval. De y-as is afgesneden zodat de verschillende uitkomsten visueel beter met elkaar vergeleken kunnen worden. De figuur (CC-BY) is gemaakt met JASP (jasp-stats.org).
De tweede en derde Vragenlijst: beoordeling van oneven versus even getallen
De eerste vragenlijst presenteerde respondenten met de fysieke vorm van individuele getallen. Wellicht beïnvloedt deze vorm (bijvoorbeeld de hoekige 4) de resultaten. Een tweede vragenlijst (met 3424 respondenten) stelde daarom de vraag meer algemeen: in hoeverre zijn (on)even cijfers ‘(Bv. 2, 4, 6, 8 of 10)’ meer mannelijk of meer vrouwelijk? De derde vragenlijst (met 5116 respondenten) was hetzelfde maar had het over (on)even getallen (‘twee, vier, zes etc.’). Figuur 3 toont de resultaten voor de tweede vragenlijst, en Figuur 4 voor de derde vragenlijst.
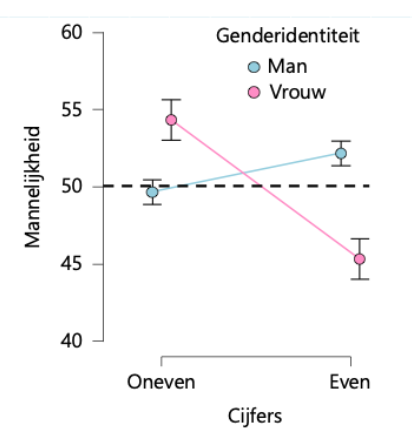
Figuur 3. Gemiddelde mannelijkheidsscores (minimum 0, maximum 100) voor ‘even en oneven cijfers’, apart voor de 2217 mannelijke en 1121 vrouwelijke respondenten die beide vragen beantwoordden. De onzekerheid rondom de gemiddelde scores is weergegeven middels een 95 procents-betrouwbaarheidsinterval. De y-as is afgesneden zodat de verschillende uitkomsten visueel beter met elkaar vergeleken kunnen worden. De figuur (CC-BY )is gemaakt met JASP (jasp-stats.org).
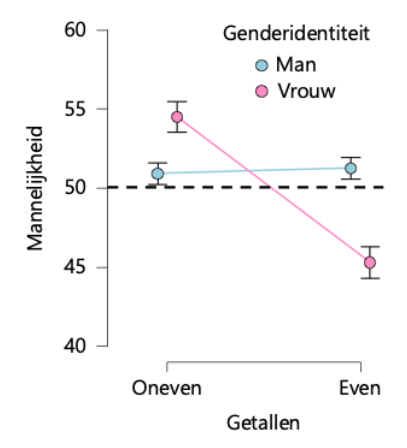
Figuur 4. Gemiddelde mannelijkheidsscores (minimum 0, maximum 100) voor ‘even en oneven getallen’ apart voor 3225 mannelijke en 1828 vrouwelijke respondenten die beide vragen beantwoordden. De onzekerheid rondom de gemiddelde scores is weergegeven middels een 95 procents-betrouwbaarheidsinterval. De y-as is afgesneden zodat de verschillende uitkomsten visueel beter met elkaar vergeleken kunnen worden. De figuur (CC-BY) is gemaakt met JASP (jasp-stats.org).
De vrouwelijke respondenten laten telkens hetzelfde resultaat zien: oneven cijfers worden als relatief mannelijk beoordeeld, en even cijfers als relatief vrouwelijk. De mannen daarentegen vinden even cijfers licht mannelijk, en laten voor de oneven cijfers een variabel patroon zien: sterk mannelijk (Figuur 2), neutraal (Figuur 3), en licht mannelijk (Figuur 4).
Conclusie
De psychoanalytische voorspelling van Jeffreys is ten dele bevestigd en ten dele ontkracht. Gemiddeld genomen beoordelen vrouwen de even cijfers als relatief vrouwelijk, en de oneven cijfers als relatief mannelijk. Dit stemt overeen met Jeffreys’ psychoanalytische voorspelling. Maar mannen laten een ander patroon zien en beoordelen de even cijfers juist als mannelijk.
Het verschil tussen de geslachten en de uitkomsten voor de individuele cijfers stellen ons voor een raadsel. Een gedetailleerde analyse van de relatie tussen de scores over de verschillende getallen kan misschien uitkomst bieden (en we moedigen de onverschrokken lezer aan zich hierin te verdiepen), maar in het licht van deze gegevens kunnen we enkel begrip opbrengen voor de toenmalige beslissing van Jeffreys om de empirische toetsing van zijn psychoanalytische theorie links te laten liggen en zich in plaats daarvan te concentreren op eenvoudigere materie, zoals de kwantummechanica en de structuur van de aardkern.
Tot slot nog een verduidelijking. Persoonlijk vinden wij Jeffreys’ psychoanalytische theorie lachwekkend onwaarschijnlijk. Haar enige aantrekkingskracht is dat ze een empirisch toetsbare voorspelling doet, en deze aantrekkingskracht was voor ons onweerstaanbaar. We denken ook niet dat deze resultaten op welke wijze dan ook relevant zijn voor de status van de psychoanalytische of psychodynamische behandelmethoden. Onze resultaten zouden eventueel wel relevant kunnen zijn voor marketing en reclame – producten voor mannen zouden wellicht gebaat zijn bij het gebruik van de getallen 1 en 5, terwijl reclamemakers bij producten voor vrouwen beter de 8 kunnen inzetten. Vervolgonderzoek is noodzakelijk om te bepalen of de abstracte associaties zich daadwerkelijk vertalen naar een hogere kans om bepaalde producten aan te schaffen. Wij blijven sceptisch.
Correspondentie over dit artikel via ej.wagenmakers@gmail.com.
De Engelstalige citaten zijn naar het Nederlands vertaald met behulp van DeepL.
